SwiGLU Activation Function 설명

안녕하세요, 오늘은 SwiGLU Activation Function에 대해 리뷰해볼까 합니다.

얼마 전에 Meta에서 발표한 LLAMA 2나 비전에서 최근 좋은 성능을 보여준 EVA-02를 포함한 많은 논문에서 SwiGLU를 채택하고 있습니다. 딥러닝을 공부하다보면 활성화 함수는 다소 사소하게 여겨질 수 있지만 실제로는 그렇지 않고, 심하게는 모델 학습이 정상적으로 되느냐 마느냐를 결정지을 수 있는 중요한 요소입니다.

 

논문: GLU Variants Improve Transformer

---

SwiGLU 배경

SwiGLU는 Swish + GLU, 두개의 Activation Functions를 섞어 만든 함수입니다.

왜 이런 함수를 설계했는지 하나씩 살펴보고 합쳐서 이해하면 좋겠습니다.

Swish Activation Function

$$ Swish(x) = x \sigma(\beta x) $$

여기서,

• \(\sigma\): Sigmoid Function \(\sigma(x) = \frac{1}{1+e^{-x}}\)
• \(\beta\): 학습 가능한 파라미터

Swish Function - 출처: https://blog.paperspace.com/swish-activation-function/

Swish Function의 몇가지 특징들을 살펴보겠습니다 (참조)

• Unbounded above for \(x \ge 0\): \(x \ge 0\) 구간에서 값의 상한이 없음
  • 모든 양수값을 허용함으로써 정보를 살려가겠다
• Bounded below \(x < 0\): \(x < 0\) 구간에서 값의 상한이 존재하며, 0으로 수렴
  • 음수값에 대해 조금의 정보를 살려 Dying(입력으로 음수가 들어오면 업데이트가 아예 이루어지지 않음)을 방지함
  • 매우 큰 음수라도 regularize 하는 효과가 있다
• Differentiability & Smoothness: 모든 구간에서 도함수가 연속 함수임
  • 기울기의 불연속 구간이 없기 때문에 oscillation이 적어 빠른 수렴이 가능합니다 (어느 지점에서 갑자기 미분값이 확확 바뀌면 수렴이 어려운 건 당연하지 않을까요?)
• Non-monotonicity: 단조 증가하지 않음 (모든 구간에 대해 미분값이 0보다 크거나 같지는 않음)
  • 설정에 따라 어디서 단조 증가하지 않는지 결정할 수 있는데, \(\beta = 1\)일 때를 기준으로 -1에서 단조 증가를 어기게 됩니다. 이는 마치 음수 구간에서의 정규화처럼 보이기도 합니다 (실제로 그렇게 해석하는건 무리가 있음).
• Self-gated: 입력의 정보량을 조절하는 기능을 함
  • LSTM에서 나온 아이디어로써, \(x\)와 \(\sigma(\beta x)\)를 분리해놓고 생각하면 쉽습니다.
    \(\sigma(\beta x)\)는 무슨 짓을 하더라도 0~1 사이의 값인데, 그 값을 결국 입력 자기자신 \(x\)가 결정하기 때문에 self-gating이라고 부릅니다. 이 또한 generalization을 돕고 overfitting을 막아줍니다.
• Computationally expensive: Sigmoid가 들어가기 때문에 오래 걸림 (지수 함수는 다 그렇습니다)

GLU (Gated Linear Units)

GLU - 출처:&nbsp;https://medium.com/@tariqanwarph/activation-function-and-glu-variants-for-transformer-models-a4fcbe85323f

$$ GLU(x, W, V, b, c) = \sigma(xW + b) \otimes (xV + c) $$

여기서,

• \(x\) : Input
• \(W, V\) : 학습 가능한 텐서
• \(b, c\) : 학습 가능한 텐서 (bias)
• \(\otimes\) : Element-wise multiplication (같은 위치에 있는 값끼리 곱함)

Swish와 마찬가지로 \(\sigma(xW + b)\)와 \((xV + c)\)를 나누어 생각하면 \((xV + c)\)가 \(\sigma(xW + b)\)의 Element-wise filter라고 이해할 수 있습니다.

• 이 함수는 자연어에서 그 효과가 먼저 입증됨
• torch.nn.GLU에 의하면 그 형태가 좀 다른데 뭐가 뭔지 잘 모르겠습니다

---

SwiGLU Activation Function

SwiGLU는 위의 두가지를 결합하여 만든 함수입니다.

$$ SwiGLU(x, W, V, b, c, \beta) = Swish_{\beta}(xW + b) \otimes (xV + c) $$

참고로 앞서 설명한 Swish, GLU의 장점 이외에 이 함수가 수학적으로 왜 우수한지는 설명하기 어렵습니다 (논문에서도 설명하지 않음).

Swish의 단점인 많은 계산량은 여전하지만 그것을 상쇄하는 장점은 역시 훌륭한 성능입니다.

 

수학이 없으니 바로 결과로 보시죠

T5 모델에서의 training step에 따른 log-perplexity

GLUE Language-Understanding Benchmark

SuperGLUE Language-Understanding Benchmark

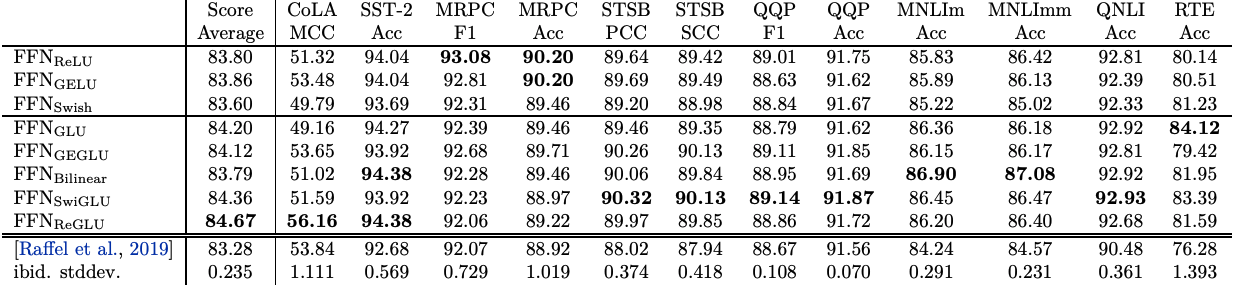
논문에서는 SwiGLU 이외에도 ReGLU, GEGLU 등을 제안하고 있어 다채로운 결과를 보여줬습니다. 단지 SwiGLU만 독보적으로 우수한건 아니고 태스크에 따라 다른 xxGLU도 좋은 성능을 보였다고 합니다.

참고로

• GEGLU: GeLU + GLU
• ReGLU: ReLU + GLU
• Bilinear: GLU에서 Sigmoid를 제외한 것

가 소개되고 있습니다.

---

SwiGLU 결론

최근 공개되는 LLM, Foundation Models에서 SwiGLU를 상당수 채택하고 있습니다.

모델을 설계하실 때 고려하시거나, 논문을 이해하실 때 도움이 될 것 같습니다.

마지막으로 PyTorch에서 SwiGLU를 어떻게 구현하는지 소개해드리고 마치겠습니다.

import torch.nn as nn
import torch.nn.functional as F

# 간단 사용법
class SwiGLU(nn.Module):
	def forward(self, x):
    	x, gate = x.chunk(2, dim=-1) # 마지막 dimension에 대해 절반으로 나눔
        return F.silu(gate) * x # SiLU는 Swish의 beta=1
        
# 혹시 Swish에서 beta를 살리고 싶다면 F.silu 대신 아래를 쓰자
class Swish(nn.Module):
	def __init__(self):
    	super().__init__()
        self.beta = nn.Parameter(torch.Tensor([1.]))
        
	def forward(self, x):
    	return x * F.sigmoid(self.beta * x)